出题人太菜，暂无测试数据。

题目描述

下雨了，灰灰坐在屋里，望着窗外地上深浅不一的水洼，陷入了沉思。
灰灰现在处在一张\(M \times N\)的地图的左下角，他的家在右上角，地图中除左下角和右上角外每个都有一定深度的积水，会会从上一格移动到下一格需要花费1s的时间。
暴雨还在继续，情况有些糟糕。每过1s时间，第\((i, j)\)格中的水都会上涨\(k\)个深度，\(k\)的值为\({(i-1, j), (i, j-1), (i+1, j), (i, j+1)}\)中有水的格子的数量（\(k \in [0, 4]\)）；特别的，若\((i, j)\)水深为\(0\)，则\(k\)始终为\(0\)
现在灰灰要挑选一条路，使得走这条路回家，经过格子的雨水深度之和最小。请你帮帮他

输入输出格式

输入格式

第一行两个整数，\(M, N\)
接下来\(M\)行，每行\(N\)个整数，表示初始时这个格子的水深

输出格式

一行两个整数，表示最小深度和与所需时间

样例

输入

3 4
1 2 3 0
2 3 4 5
0 4 5 6

输出

31 5

样例解释

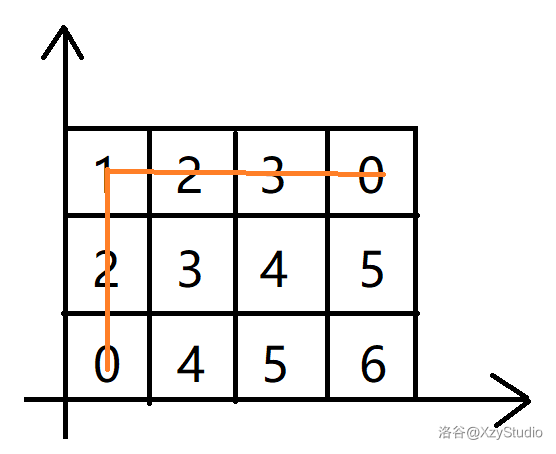
注：从\((0, 0)\)迈上\((0, 1)\)时\((0, 1)\)从\(2\)涨到\(4\)。\(ANS = 4+5+11+11 = 31\)

数据范围

对于所有数据，\(3 \leqslant N, M \leqslant 1000\)，且所有深度之和不超过\(10^9\)