数据生成器：

#include<bits/stdc++.h>
using namespace std;
const int N=100,inf=1e9;
mt19937 rnd(time(0));
int n;
int main(){
    freopen("travel9.in","w",stdout);
    cout<<N<<"\n";
    for(int i=1;i<N;i++){
        for(int j=1;j<=N-i;j++) cout<<rnd()%N+1<<" ";
        if(i<N) cout<<"\n";
    }
    return 0;
}

CF773D

考虑观察性质。

首先，生成树一定可以形如一条链加一个菊花，且链与菊花的连接处为原图的最小边权。

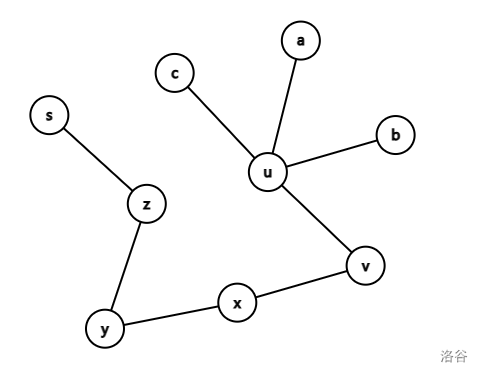
证明：不妨设 \((u,v)\) 这条边权值最小，则若 \((v,s)\) 上存在其他边，则将其移动到菊花上一定更优，该点的贡献会变为 \(w(u,v)\) 。

而对于 \(u\) 方向的边，若将其一端改为 \(u\) 点，代价不变。

不妨将所有边权减去 \(w(u,v)\) ，最终答案加上 \((n-1)w(u,v)\) 。显然菊花端的点贡献均为 \(0\) 。

我们证明从 \(s\) 到 \(u\) 的边权一定单调不降，除了 \((x,y)\) 与 \((x,v)\) 的关系之外。不妨设 \((z,y)\) 是从 \(s\) 开始，链上**第一个**大于上一条边（即 \((s,z)\)）的边。

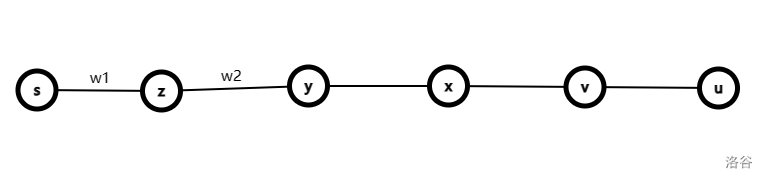
\(w1<w2\) ，则此时代价一定 \(\ge 2w_1\) ，我们将 \(z\) 与 \(v\) 连边，中间的点都连接到 \(v\) 上，此时不管 \(w3\) 与 \(w1\) 的大小关系，代价一定 \(\le 2w_1\) 。

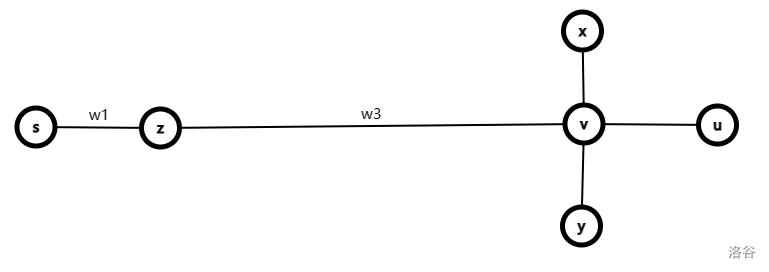
因此，总代价 \(=w(s,z)+w(z,y)+\dots+w(y,x)+\min(w(y,x),w(x,v))=w(s,z)+w(z,y)+\dots+\min(2w(y,x),w(y,x)+w(x,v))\) 。

此时的问题等价于 \(s\) 到 \(v\) 的最短路，初值 \(d_u=\min(w(v,u)+2w(u,x))\) 。进行 dij 即可。因为原图是稠密图，可以做到 \(O(n^2)\) 。

std

#include<iostream>
#define int long long
using namespace std;
const int N=2e3+5;
int n,c=1e9+7,u;
int a[N][N];
int d[N],vis[N];
void dij(int u){
    for(int i=1;i<=n;i++){
        d[i]=a[i][u];
        for(int j=1;j<=n;j++){
            if(i==j) continue;
            d[i]=min(d[i],a[i][j]*2);
        }
    }
    for(int i=1;i<=n;i++){
        int p=1e9+7,v=0;
        for(int j=1;j<=n;j++){
            if(vis[j]) continue;
            if(d[j]<p){
                p=d[j];
                v=j;
            }
        }
        vis[v]=1;
        for(int j=1;j<=n;j++){
            if(vis[j]) continue;
            d[j]=min(d[j],d[v]+a[v][j]);
        }
    }
}
signed main(){
    freopen("travel.in","r",stdin);
    freopen("travel.out","w",stdout); 
    ios::sync_with_stdio(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            cin>>a[i][j];
            if(a[i][j]<c){
                c=a[i][j];
                u=i;
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            a[i][j]-=c;
            a[j][i]=a[i][j];
        }
    }
    dij(u);
    for(int i=1;i<=n;i++) cout<<d[i]+(n-1)*c<<"\n";
    return 0;
}