1 条题解
-
0
 XzyStudio (admin)
LV 8
MOD
RP++
tayz
@ 2024-11-27 19:55:32
XzyStudio (admin)
LV 8
MOD
RP++
tayz
@ 2024-11-27 19:55:32
解题思路
首先,因为莫比乌斯带是一个单侧曲面,我们可以将其展开并看做一个**周长为 \(2L\) 的圆**,两个质点此时就处于**圆上一条直径的两侧**。
这时候,我们不妨用初中物理公式来表示**两个质点在某一时间的位移**,及 \(x = v_0t + \frac12at^2\) ,所以 \(x_1 = v_1t + \frac12a_1t^2\) , \(x_2 = v_2t + \frac12a_2t^2\)。
那么,可以由此写出两个质点的**位移差** \(\Delta x = x_1 - x_2 = (v_1t + \frac12a_1t^2) - (v_2t + \frac12a_2t^2)\),用 \(\Delta v\) 表示两质点的**速度差** \(v_1 - v_2\),\(\Delta a\) 表示两质点的**加速度差** \(a_1 - a_2\),所以 \(\Delta x = \frac12\Delta at^2 + \Delta vt\)。
设函数\(f(t) = \frac12\Delta at^2 + \Delta vt\),因为圆形的周长为 \(2L\) ,两个质点刚开始相距的弧长为 \(L\),故不难得出**相遇的条件**是 \(f(t) = 2kL - L \ (k\in Z)\)。
此时,思路瞬间就明了了,**符合条件的 \(k\) 的个数就是最终要求的** \(ans\)。但是,如何采取一个高效的方法,使得能在 \(10^{18}\) 这样庞大的数据范围内求出 \(k\) 的取值范围仍然是一个问题。
我们仔细研究函数 \(f(t)\) 的性质,由于 \(f(t)\) 是二次函数,那么它一定在 \([0,+\infin)\) 上可以被分为**至少一个单调区间**,我们只需要**分类讨论** \(\Delta v\) 的**正负性**,即可找到这些单调区间。
注:对于 \(\Delta a < 0\) 的情况,我们可以将 \(\Delta a , \Delta v\) 同时取反,对于 \(\Delta a = 0\) 的情况,我们可以将 \(\Delta v\) 取绝对值,所有的情况如下图所示。
\(\Delta v > 0\) 时:\
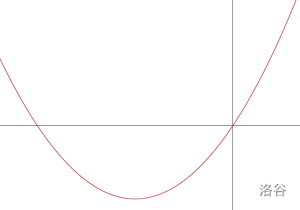 \
\
\(\Delta v < 0\) 时:\
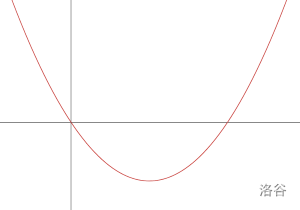 \
\
\(\Delta a = 0\)(一次函数)时:\

找到单调区间后,我们就可以根据函数在**某一区间上的最大值和最小值**反推出 \(k\) 在这个区间上的**十分近似的取值范围**,从而通过**极低次数的枚举** \(k\) 的取值范围,由于 \(k\) 的**取值集合是连续的**,故可以通过取值范围得到答案。
至于求前 \(10^6\) 个相交时间 \(t_i\),只需**枚举 \(k\) 值并通过公式法解二次方程**即可。注意因为 \(10^6\) 的数据和过大的常数,排序 \(O(nlogn)\) 的复杂度可能会导致超时,因此 \(k\) 值的枚举**应按照一定的顺序**以确保输出的 \(t_i\) 递增。
标程代码
#include <bits/stdc++.h> #define long __int128 #define a 1.0/2*dta #define b dtv using namespace std; const int maxn = 1e6; long L, t, v1, v2, a1, a2; long dtv, dta, ans, mid, r; __int128 _abs(__int128 x) { if (x > 0) return x; else return -x; } long getk(long num) { //反推k值,取整数 return (1.0*num/L+1)/2; } double f(long x) { //求f(x)的值 return a*x*x + b*x; } double delta(int k) { //求delta return b*b + 4*a*(2*k*L - L); } double getminx(double k) { //二次方程解的小值 return 1.0 * (-b - sqrt(delta(k))) / (2*a); } double getmaxx(double k) { //二次方程解的大值 return 1.0 * (-b + sqrt(delta(k))) / (2*a); } long fast_read() { long x = 0, f = 1; char ch = getchar(); while (ch > '9' || ch < '0') { if (ch == '-') f = -f; ch = getchar(); } while (ch <= '9' && ch >= '0') { x = x * 10 + (long)(ch -'0'); ch = getchar(); } return x * f; } void fast_write(long x) { if (x == 0) return; fast_write(x / 10); putchar(x % 10 + '0'); } void solve() { dtv = v1 - v2, dta = a1 - a2; if (dta < 0) dta = -dta, dtv = -dtv; if (dta == 0) dtv = _abs(dtv); if (a == 0 && b == 0) { printf("%d", 0); return; // 答案一定为 0 } if (b >= 0) { // 对称轴 <= 0 r = getk(f(t)); ans = r; // = r - 1 + 1 左边最小一定是1 if (ans == 0) printf("%d", 0); else fast_write(ans); printf("\n"); for (int i = 1; i <= r && i <= maxn; i++) if (a == 0) printf("%.8lf\n", (1.0*2*i*L-L)/dtv); //一次函数 else printf("%.8lf\n", getmaxx(i)); //二次函数 } else { // 对称轴 > 0 double axis = -1.0*b/(2*a); //函数对称轴 long mini = f(axis); //函数最小值 mid = getk(mini), r = getk(f(t)); while (delta(mid) < 0) mid++; //找到第一个符合条件的k值 if (delta(mid) == 0) ans = -1; //两个解在同一点,会重复计算 ans += -mid + 1; // = 0 - mid + 1 左边k最小一定是0 ans += r - mid + 1; if (ans == 0) printf("%d", 0); else fast_write(ans); printf("\n"); int cnt = 1; // i 从 0 枚举到最低点,再枚举到最高点确保答案递增 for (int i = 0; i >= mid && cnt <= maxn; i--, cnt++) printf("%.8lf\n", getminx(i)); // i = (delta(mid) == 0)?mid+1:mid 确保不会重复输出 for (int i = (delta(mid) == 0)?mid+1:mid; i <= r && cnt <= maxn; i++, cnt++) printf("%.8lf\n", getmaxx(i)); } } int main() { // 用较快输入输出方式 L = fast_read(), t = fast_read(); v1 = fast_read(), a1 = fast_read(); v2 = fast_read(), a2 = fast_read(); solve(); return 0; }数据生成器代码
本题数据使用 python 生成。
import cyaron from cyaron import * # 引入CYaRon的库 _n = ati([100, 1E4, 1E6, 1E6, 1E6]) _m = ati([100, 1E4, 1, 1E6, 1E6]) _k = ati([10, 1, 1E9, 1E9, 1E9]) _h = ati([100, 1E6, 1E18, 1, 1E18]) def run(): for num in range(0, 5): for i in range(0, 3): data = IO(file_prefix="writer", data_id=num*3+i+1) n = cyaron.randint(1, _n[num]) m = cyaron.randint(1, min(n,_m[num])) k = [] h = [] for j in range(0, n): k.append(cyaron.randint(1, _k[num])) h.append(cyaron.randint(1, _h[num])) data.input_writeln(n, m) data.input_writeln(k) data.input_writeln(h) data.output_gen("E:\\MyProblems\\writer\\writer_right\\writer.exe")
- 1
信息
- ID
- 1094
- 难度
- 9
- 分类
- (无)
- 标签
- (无)
- 递交数
- 1
- 已通过
- 1
- 通过率
- 100%
- 上传者